Apr-19-2015 Lab 13: Impulse-Momentum activity

Introduction: Impulse combines the applied force and the time interval over which that force acts.

For a constant force F acting over a time interval t, the impulse J = F*t.  

However, if the force is not constant, we can still calculate the impulse as the area under the force vs. time graph. 

The impulse-momentum theorem states that the amount of momentum change for the moving cart is equal to the amount of the net impulse acting on the cart.

our purpose of this lab is to test this idea.

EXPT 1: Observing Collision forces that change with time.

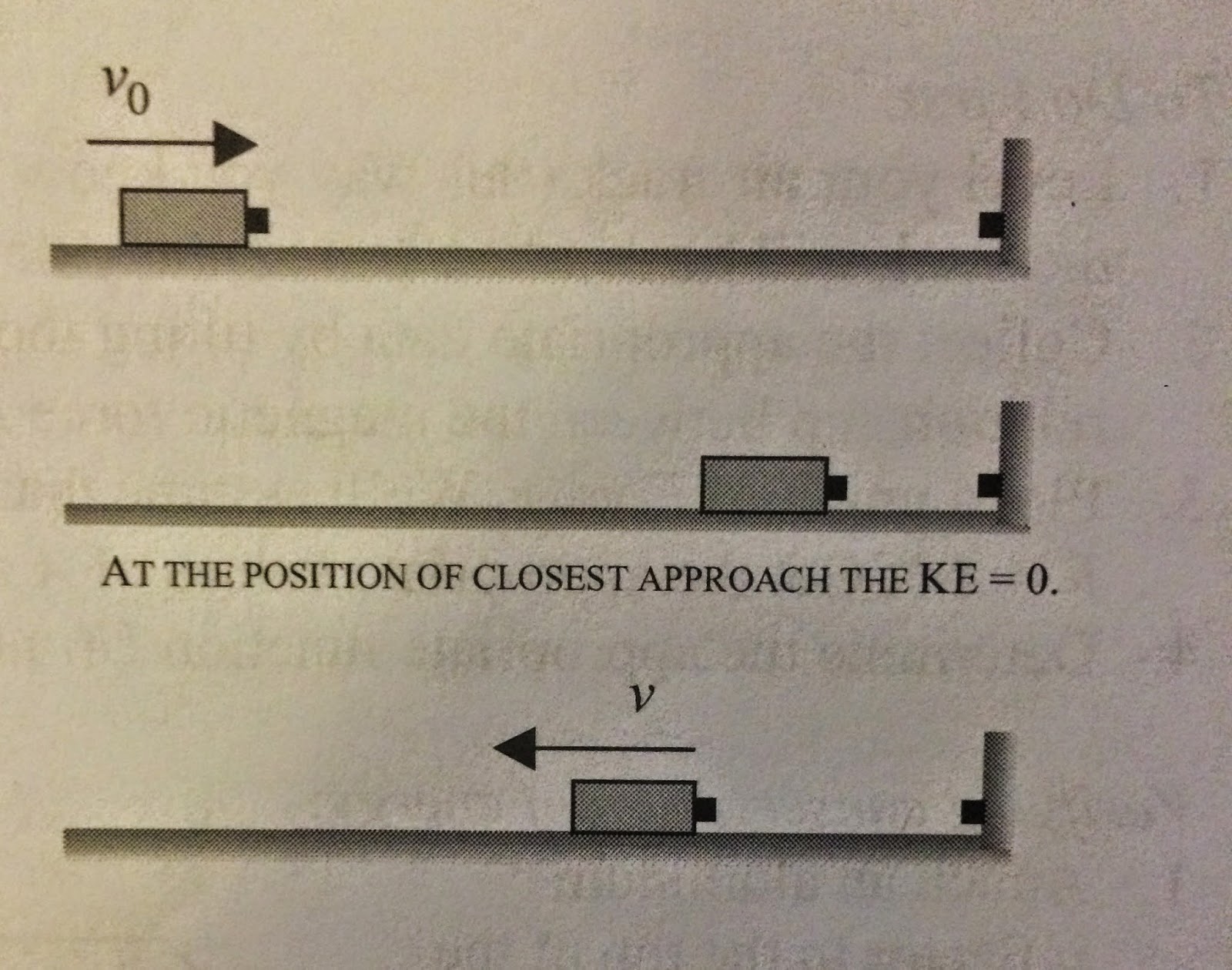
First, set up like the picture: 

we could measure the impulse acting on the cart by taking the area under the force vs time graph for the collision, and measure the change in momentum of the cart by knowing its mass and measuring its velocity before and after the collision using the motion detector. 

1. Fasten the force probe securely to the cart so that the rubber stopper extends beyond the front of the cart. set the positive direction is toward the right. 

2. set up the motion detector. be sure that the ramp is level. 

3. We measured the mass of the cart and sensor m = 0.635 kg.

4. Open the experiment file called Impulse and Momentum.cmbl, set up to record force and motion data at 50 data points per second. 

5. zero the force probe and begin graph. then give the cart a push toward the wall. 

after we did by following the steps, we got the graph:

red line is the graph of Force vs. time.

this blue line is the graph of position vs. time.

this blue line is the graph of velocity vs. time.

From this graph, after we integral the graph of force vs. time we got the area A = -0.3952. 

after we liner fit the graph of position vs. time before the collision, we got the slope m = 0.3615 which states the cart's velocity before the collision v(0) = m = 0.3615 m/s

after we liner fit the graph of position vs. time after the collision, we got the slope m = -0.2790 which states the cart's velocity after the collision v(f) = m = -0.2790 m/s

Then, we did the calculation to test that the impulse is equal to momentum or not.

we could see the impulse J = mv(f) - mv(0) = -0.4067 is very close to the area under the graph of   force vs. time which states the momentum. 

EXPT 2 : A larger Momentum change.

this experiment is same as experiment 1 but add 200 grams of mass to our cart. m = 0.835 kg.

Repeat the experiment using a more massive cart. record the appropriate data and graphs.

red line is the graph of Force vs. time.

this blue line is the graph of position vs. time.

this blue line is the graph of velocity vs. time.

From this graph, after we integral the graph of force vs. time we got the area A = -0.6621. 

after we liner fit the graph of position vs. time before the collision, we got the slope m = 0.4435 which states the cart's velocity before the collision v(0) = m = 0.4435 m/s

after we liner fit the graph of position vs. time after the collision, we got the slope m = -0.3622 which states the cart's velocity after the collision v(f) = m = -0.3622 m/s

Then, we did the calculation to test that the impulse is equal to momentum or not.

For this experiment,  the impulse J = mv(f) - mv(0) = -0.6728 is still very close to the area under the graph of  force vs. time which states the momentum. 

EXPT 3 : Impulse-Momentum theorem in an inelastic collision.

It is also possible to examine the impulse-momentum theorem in a collision where the cart sticks to the wall and comes to rest after the collision.

leave the extra mass on cart so that its mass is the same as expt 2.  m = 0.835 kg.

we predict that the impulse is same as the nearly elastic collision. and we predict that the impulse is equal to the momentum. 

red line is the graph of Force vs. time.

this blue line is the graph of position vs. time.

this blue line is the graph of velocity vs. time.

From this graph, after we integral the graph of force vs. time we got the area A = -0.1763. 

after we liner fit the graph of position vs. time before the collision, we got the slope m = 0.22 which states the cart's velocity before the collision v(0) = m = 0.22 m/s

after the cart hits the wall, it comes to rest. v(f) = 0.

Then, we did the calculation to test that the impulse is equal to momentum or not.

For this experiment,  the impulse J = mv(f) - mv(0) = -0.1837 is still very close to the area under the graph of  force vs. time which states the momentum.

Conclusion:

For those three experiments, all of the impulses we calculated and all of the areas under the graph of  force vs. time are very close. If we could ignore some uncertainties (which like air friction,etc.), we could say that the impulse-momentum theorem can be used on those three conditions.  

Apr-19-2015 Lab 12: Magnetic Potential Energy Lab

The set up:
A frictionless cart with a strong magnet on one end approaches a fixed magnet of the same polarity:

For this lab, our goal is verify that conservation of energy applies to this system.

To do first:
we will use a glider on an air track as our cart on a frictionless surface. if we raise one end of the air track the cart will end up at some equilibrium position, where the magnetic repulsion force between the two magnets will equal the gravitational force component on the cart parallel to the track.

We measured the mass of air track m= 0.354 kg.







we measured 4 sets of data about the r and the angle between ground and the air track.

because the magnetic repulsion force between the two magnets will equal the gravitational force component on the cart parallel to the track, we got F=mg*sinθ. 

then we could calculate the force F from the θ we measured.










Open the program, we put the 4 sets of force and r into the program, then we got the graph of F vs. r. we will assume that the relationship takes the form of a power law: F = Ar^n.

After curve fit our graph, we got two equations about force F and work done U(r) which come from the interaction between the magnets:

Right now, we are verifying conservation of energy:

We measured the separation distance between the magnets d= 0.28 m.

now, we have a way to measure both the speed of the cart "velocity" and the separation between the magnets at the same time.  However, For this part, the r should be the distance between the magnet on the air track and the sensor. so that r = "position" - d.

then we set the calculated column:
PE = U(r) = 0.006754 * r^(-1.349)

KE = 1/2 * m * "velocity"^2

Total energy TE = KE + PE

Start with the cart at the far end of the track. Start the detector, then give the cart a gentle push.

after we done with experiment, we got the graph like this :

yellow line is the graph of TE vs. time


Purple line is the graph of PE vs. time


Red line is the graph of KE vs. time




Conclusion:

For this experiment, there should no any energy will lose. so the KE of air track for the time before the collision should be same as the time after the collision. However,They are not same on our graph.
From this result I think our set up may not perfect, or our separation distance may not exactly correct, or we may made some mistakes we did not know during the experiment.  This experiment requires frictionless, but we cant completely ignore the air friction. All of those things could affect the result.

Apr-18-2015. Lab 11 : Conservation of energy----Mass-spring System

For this lab, We will be looking at the energy in a vertically-oscillating mass-spring system, where the spring has a non-negligible mass.

Before we can actually to do the lab there is some preliminary stuff to work out.

assume that the gravitational PE = 0 at the ground, and that you have a spring whose top is held fixed at a height H above the ground, and the bottom of the spring is at a position y above the ground.











there is the picture show that the GPE of the spring is mg(H+y)/2 be written as m(spring)/2 *g*H + m(spring)/2 *g*y:

Now put the origin at the top of the spring and call downward the positive direction, assume that the spring has a length L, the top of the spring is held at rest but that the bottom end of the spring is moving at a speed v downward.
there is the picture show that the KE of the moving spring is 1/2 *(1/3 *m(spring))*v^2.

then set up the spring, a 50-gram mass hanger, with the motion detector on the floor. we measured the length of the spring L = 0.485 m, the mass of the spring m(spring) = 0.24 kg.

First, we need to Determining the Spring constant of the spring.

mount a table clamp with a vertical rod to the table. mount a horizontal rod to the vertical rod. Put the Force sensor on the horizontal rod with the loop of the sensor pointing downward.


place a 50-gram the mass hanger so that it is vertical and the spring is just unstretched. zero the sensor with the mass hanger in this position.






Open the program, start collecting data and slowly pull down on the 50-gram mass . then we got the graph of Force vs. position.

after we liner fit the graph, we got the slope which is the constant of spring K = -8.03 N/m .


Right now, we need To do:
      Hang 250-grams on the mass hanger. After the spring is not stretch any more, we measured the y(0) = 0.73 m.

we have expressions of KE, GPE, PE that we worked out before:

we have the mass of the spring m(spring) = 0.24 kg  ,
the constant of the spring K = -8.03 N/m,    mass of hanging M = 0.25 kg.    y(0) = 0.73 m,
△y = 0.843 - "position"(we could measure it from the sensor)
the velocity v (we could measure it from sensor).

Under the Data menu in loggerPro, we created:
the New calculated column of KE = 1/2 *(M + 1/3 *m(spring))*v^2.
the New calculated column of GPE = (M + m(spring)/2) * g * "position" .
the New calculated column of EPE = 1/2 *K *△y^2 

Then, Pull the spring down about 10 cm and let go. we got the graphs:

this blue graph is the graph of KE vs. time.



this purple graph is the graph of GPE vs. time.



this green graph is the graph of EPE vs. time.

 this blue graph is the graph of KE vs. position.



this purple graph is the graph of GPE vs. position.



this green graph is the graph of EPE vs. position.

this blue graph is the graph of KE vs. velocity.



this purple graph is the graph of GPE vs. velocity.



this green graph is the graph of EPE vs. velocity.



Finally: create a new column called TE(Total Energy), which is the sum of the KE, GPE, EPE.

this is graph of TE vs. time.

the min of TE = 2.242 J
the mean of TE = 2.309 J.
the max of TE = 2.377 J


this is graph of TE vs. position.



this is graph of TE vs. velocity.





Conclusions:

From those graphs, we could know about the energy in a vertically-oscillating mass-spring system, where the spring has non-negligible mass.  The potential energy will be greatest when the spring is stretched or compacted. However, KE + GPE + EPE should be always same so the total energy is conserved. the graph of the total energy should be a straight line. Although our result of the graph of the total energy is a line which has small wave, the min of TE is very close to the max of TE, which means our measurements are not bad.

Apr-18-2015. Lab 10: Work-Kinetic Energy Theorem Activity

This lab has three experiments. We could text the Work-Kinetic Energy Theorem Activity by those 3 experiments. 

Expt 1 : Work done by a nonconstant spring force.

For this experiment, we will measure the work done when we stretch a spring through a measured distance.

consider a cart being pulled by a horizontal force along a horizontal surface:
         for a nonconstant force, sketch a graph of F vs. X.
then we will be able to calculate the work done by finding the area under this graph.

First,

after we did the experiment file by following steps, we got the graph of Force vs, Distance:

then  we liner fit the graph, we have a slope A = 1.842 +-0.0109 which equals to the constant K of our spring. In addition. we integral this graph between 0.06m and 0.2m  I = 0.03382 m*N which equals the area between 0.06m and 0.2m. 

otherwise, By the work done formula:

the work done U(x) that we calculated almost equals to the area of Force vs. Distance graph between 0.06m and 0.2m.

Expt 2 : Kinetic Energy And The Work-Kinetic Energy Principle.

We were using the same set up as the experiment 1.

we measured the mass of the cart m= 0.573 kg.

For this expt, we need to use the New calculated column to calculate the kinetic energy of the cart at any point : KE(J) = 1/2 * m * v^2 

Make sure that the x-axis of our graph is position, and Zero the force probe with the spring hanging loosely. Then pull the cart along the track so that the spring is stretched about 1 m from the unsretched position as same as the expt 1. we will get the graph like:

After we did this experiment by following steps, and we putted the Force vs. Position graph and KE vs. Position graph into the together, we got the graph:

the purple line means Force vs, Position. the black line means KE vs, Position.

we got the work done I= 0.07395 m*N by finding the area under the curve using the integration routine between position 0.241m and 0.3m. 
And we got the change in kinetic energy of the cart after it is released from the initial position to the position 0.241m by using the analysis feature of the software. the kinetic energy = 0.074J

For the conclusions, the work done I= 0.07395 on the cart by the spring equals to its change in the kinetic energy= 0.074.


Expt 3 : Work-KE theorem.

On the Professor's computer, we watched the movie Work KE theorem cart and machine for Phys 1.mp4.  In the video, the professor uses a machine to pull back on a large rubber band. The force being exerted on the rubber band is recorded by an analog force transducer onto a graph.

At the move, make a careful sketch the force vs. position graph like the picture:

Use the data, we calculated the total area A(total) = 26.595 J.
Use the formula, we calculated the final KE = 23.89 J. 

Conclusion:

For this experiment, the A(total) should be very close to the KE,  however, there are not very close. I think there are some reasons: the lines are not straight at all from the video, our graph may have small difference from the video,

Apr-14-2015. Lab 9 : Centripetal force with a motor

The apparatus is described below. As the motor spins at a higher angular speed w, the mass revolves around the central shaft at a larger radius and the θ increases. 

our job is to come up with a relationship between w and θ . 
1. we can get the θ from looking at the right triangle with hypotenuse L and height (H-h)s. like the picture. we got the θ= cos^(-1)(H-h/L) . 

2. we can get w from timing how long it takes for the stopper to make 10 revolutions around the shaft.

we measured the L= 1.654m, R= 0.97m, H= 2m by the meter ruler.


3. we can get h by putting a horizontal piece of paper or tape on a ring stand and slowing raising the piece of paper of paper until the stopper just grazes the top of it as it passes by.

then, we got 5 sets of different data to test our model by collecting values of h at a veriety of values of w.
In addition, we calculated 5 sets of different w and θ .





Here is the force diagram:

we got the relationship between w and θ(we already know the R= 0.97m, L= 1.654m, and g= 9.8m/s^2).
set the equation of the relationship between w and θ to y = x. 

then, we put the 5 different θ into this equation to get 5 new w. Now we got the y which means 5 sets of w from timing how long it takes for the stopper to make 10 revolutions around the shaft, we got the x which means 5 sets of w from that we put the 5 different  θ which we calculated from θ=cos^(-1)(H-h/L) into the equation of the relationship between w and θ.  

open the Excel, input all data and make both y and x square. then linear fit the graph. 





From the picture, we got y = 0.9827x. we could see the slope is 0.9827 which means y is almost equal to x.















For this lab, we find the relationship between w and θ . and we got 5 sets of data to test our model by collecting value of h(which we could calculated the θ) at a variety of values of w. the final result y= 0.9827x shows that w will increase with the θ's increase.

Apr-13-2015, Lab 8 : Demonstration-Centripetal Acceleration vs. Angular Frequency

This lab's purpose :  To determine the relationship between centripetal acceleration and angular speed.

Setup:
1. Place the accelerometer on the disk.  Verify that the accelerometer reads 0 in the x and y-directions and -9.8m/s^2 in the z-direction.
2. Spin the disk at some speed. Verify that the accelerometer reads 0 in either the x or the y-directions and something in the other direction.

Measurements we will make :

1. How long it takes for disk to make some number of rotation at a range of rotational speed.

2. The accelerometer reading corresponding to each rotational speed.

3. Distance of the accelerometer from the center of the rotation disk.

we measured the radius r = 14cm from ruler.

then, we need to test.
from the centripetal force formula, we got the relationship between Acceleration and angular speed^2 :

we measured the 5 different set of data with different power from the experiments. we got  the first rotation of time, the last rotation of time, the number of rotations, and the acceleration a.


Then use the formula to calculate the period T and the angular speed w:

T = [t(the last rotation) - t(the first rotation) ] / the total rotations 

 
W = 2pi / T























Then open the program on the computer, put all the data into the program. make the acceleration a as x-axis, make the w^2 as the y-axis. and linear fit the graph of the relationship between acceleration and angular speed^2 :

we got the slope m = 0.1361m from the graph.  However, from the centripetal force formula we got  
        a= r*w^2      which means the slope m should be equal to the radius r.


For this lab, we calculated the radius r = 0.1361m from what theory predicts, this result is pretty close with the radius we measured r = 14cm = 0.14m.  The magnitude of the centripetal acceleration is related to the tangential speed and angular velocity as follows:
                                      F = m*a = m*w^2 *r   =>   a = w^2 * r.

Apr-13-2015 , lab 7: Trajectories

This lab's purpose : To use your understanding of projectile motion to predict the impact point of a ball on an inclined board.

1. First, we need to prepare some materials : Aluminum, steel ball, board, ring stand, clamp, paper, carbon paper. then set up the apparatus as shown.

2. Launch the ball from a readily identifiable and repeatable point near the top of the inclined ramp. Notice where it hits the floor.
3. Tape a piece of carbon paper to the floor around where the ball landed. launch the ball about five times from the same place as before and verify that ball lands in virtually the same place each time.
4. Determine the height of the bottom of the ball when it launches(h=0.94m), and how far out from the table's edge it lands(x=0.553m).
5. Determine the launch speed of the ball from our measurements.
here is our calculation :


We got the launch speed of the ball is V(0) = 1.26 m/s.

6. Imagine attaching an inclined board at the edge of the lab table such that the picture:

now the ball, launches at the same spot as before, will strike the board a distance d along the board. Derive an expression that would allow us to determine the value of d. (we already know the V(0)=1.26 m/s and measured the angle a = 48' +- 1').



Then we predict the value of d from the formula. Here is our calculation:

we got the predict values of the d = 0.538m,  the x = 0.359m,  the y = 0.399m after calculated.

We also measured the value of y = 0.38m +- 0.02m by the materials.
Determine the experimental value of our landing distance d and report our experimental value as d +- dd. Here is our calculation:

we got the d +- dd = 0.5113m +- 0.0324m. 

For this lab, we got the close results between the experimental value of our landing distance d and the value of the predict. we could say that this experiment is successful.